AlphaGeometry: DeepMind's Mathematical Artist - How AI Learned to Paint with Geometric Proofs
As promised in my previous blog about DeepSeek-R1 and current LLMs' abilities to reasoning, I would like to deep-dive into AlphaGeometry - an impressive break-through of how LLM reasons math problems
For decades, automated theorem proving has been a "grand challenge" in Artificial Intelligence. It's not just about crunching numbers; it requires logical reasoning, strategic thinking, and a kind of creativity that's been difficult to capture in machines. Geometry, in particular, has presented a unique hurdle due to the complexities of translating visual and spatial relationships into a format computers can understand. But in 2024, Google DeepMind's AlphaGeometry had made a major breakthrough, achieving near-gold-medal performance on International Mathematical Olympiad (IMO) geometry problems without relying on human-provided solutions. This is a significant leap, and it signals a new era in AI's ability to tackle complex mathematical reasoning.
About the author
The project was conceived and spearheaded by Trieu H. Trinh at Google DeepMind as his "passion project." Over four years, Trinh built the system from the ground up, viewing it as "only the first deliverable of a longer-term vision." The project benefited from a unique industry-academia collaboration, with guidance from Thang Luong and Quoc V. Le at Google, and He He at New York University.
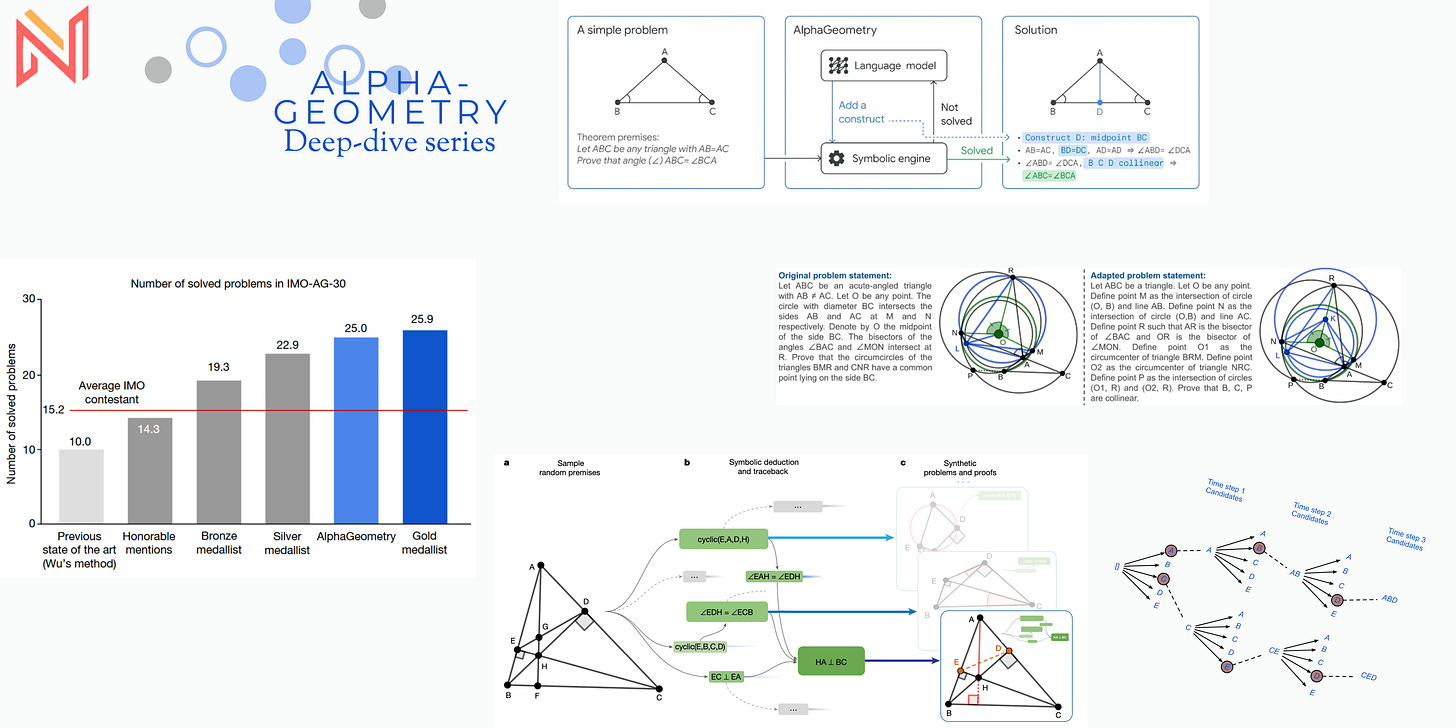
What did AlphaGeometry do?
On a benchmark set of 30 geometry problems from the IMO (2000-2022), AlphaGeometry solved 25 within the standard competition time limits. This approaches the performance of an average human gold medalist (who solved 25.9 problems on average) and dramatically outperforms the previous best automated system (Wu's method), which solved only 10.
How does it work?
Input
AlphaGeometry starts with a problem stated in a specialized, formal language representing Euclidean plane geometry. This language is designed to be understandable by the system and similar to the format used in interactive graphical proof assistants. It defines points, lines, circles, and relationships between them (e.g., "A, B, C are collinear," "AB = CD," "∠ABC is a right angle").
Initial Symbolic Deduction
The symbolic deduction engine takes the initial problem premises and applies a set of predefined geometric rules (like those found in a geometry textbook – e.g., rules about congruent triangles, parallel lines, circle properties, etc.). This includes:
Deductive Database (DD): This uses geometric rules represented as Horn clauses. For instance, a rule might state: "If A, B, and C are collinear, and B, C, and D are collinear, then A, B, C, and D are collinear."
Algebraic Rules (AR): perform algebraic calculation such as angle and distance calculations.
The engine exhaustively deduces all possible new facts from these premises, creating a growing "deduction closure" – a graph of interconnected statements.

If the symbolic engine can reach the problem's conclusion (the statement to be proven) through direct deduction, the problem is solved. However, many Olympiad-level problems cannot be solved this way. They require a "leap" – the introduction of an auxiliary construction.
Auxiliary construction
When the symbolic engine gets stuck (no new deductions can be made, and the goal hasn't been reached), the neural language model comes into play.
The language model is a transformer-based model, similar in architecture to large language models used for text generation. It's been pre-trained on the vast synthetic dataset of geometry problems and proofs.
The language model takes the current state of the problem (premises, existing deductions, and the goal) as input and predicts a single auxiliary construction. This could be:
Adding a new point (e.g., "Construct point D as the midpoint of BC").
Drawing a new line (e.g., "Construct line AD").
Defining a new circle (e.g., "Construct the circumcircle of triangle ABC").
The language model doesn't guarantee that the suggested construction is correct or helpful. It's making an "educated guess" based on patterns it learned from the synthetic data. This step is analogous to human intuition when it came to the step of proof.
And finally, the process (deduction -> potential stuck point -> language model suggestion -> incorporation) repeats in a loop.

But if the model found many possible constructions at each step, how it can be choose the most promise one?
AlphaGeometry uses a technique called "beam search." It explores the k most promising constructions (where k is a predefined "beam width," 512 in their experiment), maintaining multiple "proof branches" in parallel.
By evaluating a beam search tree of multiple different steps, more possible theorems and proofs can be generated.
Then, the loop continues until one of two things happens:
Success: The symbolic engine, in one of the proof branches, reaches the problem's conclusion. A solution (proof) has been found.
Timeout: A maximum number of iterations is reached without finding a solution. ⇒ SOLVING FAILED
Proof Output
When a solution is found, AlphaGeometry outputs the sequence of deduction steps and auxiliary constructions that led to the proof. This proof is human-readable (though sometimes verbose) and can be verified independently. The proof are arranged with symbolic steps intermixed with language model.

Training Data Generation
One of AlphaGeometry's most innovative aspects is how it generates its own training data without human demonstrations. The process involves:
Generating 1 billion random geometric diagrams using constructive actions (e.g., taking midpoints, intersections, etc.)
Using the symbolic engine to discover all possible true statements about each diagram
Employing a "traceback" algorithm to identify minimal proofs and necessary auxiliary constructions
After deduplication, this yielded 100 million unique theorem-proof pairs, with 9 million involving auxiliary constructions
Technical Details
The language model component uses:
A transformer architecture with 12 layers
Embedding dimension of 1,024
8 attention heads
151 million parameters total
Context length limited to 1,024 tokens
Trained using a cosine learning rate schedule
Some key takeaways
AlphaGeometry mimics some aspects of human problem-solving (deduction, auxiliary constructions) but relies on fundamentally different mechanisms (statistical prediction, exhaustive search).
AlphaGeometry's strength lies in its ability to perform a vast number of deductions quickly and systematically, exploring a large solution space. Humans strength lie in deep intution to perform steps, and generalize that to wider set of solutions.
AlphaGeometry's "creativity" is data-driven, while human creativity is more conceptual and can draw on a broader range of knowledge.
AlphaGeometry's output (proofs) are more explicit and verifiable, but sometimes less insightful than a human-written proof.
Limitations and Future Challenges
Despite its impressive performance, AlphaGeometry has several limitations:
It operates in a specialized formal language, not natural language like human mathematicians
It cannot handle certain types of geometry problems (like geometric inequalities or combinatorial geometry)
Its proofs are sometimes more verbose and less elegant than human proofs
It lacks access to higher-level mathematical concepts that humans use (like complex numbers or coordinate geometry)
The system requires significant computational resources (512 parallel workers for beam search)

Looking Ahead: AlphaGeometry 2
While AlphaGeometry's achievements are impressive, Google DeepMind has already taken the next step with AlphaGeometry 2, announced in early 2025. This new version makes a remarkable leap forward, solving 42 out of 50 IMO geometry problems from 2000-2024 and achieving true gold-medal performance.
The improvements in AlphaGeometry 2 - including a more expressive domain language, enhanced symbolic engine, integration with Gemini architecture, and novel search algorithms - point to an exciting future where AI systems can tackle increasingly complex mathematical challenges in fundamentally new ways.
Stay tuned for our deep dive into AlphaGeometry 2 and what it means for the future of AI in mathematics.
References:
https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/